Example - Regula Falsi method

Task 1 

MetodaThe Regula Falsi tomethod numerycznais technikaa służącanumerical dotechnique znajdowaniafor miejscfinding zerowychzeros funkcjiof ciągłeja wcontinuous danymfunction przedziale.on Łączya onagiven zaletyinterval. metodyIt bisekcjicombines ithe metodyadvantages siecznych,of oferującthe zarównobisection zbieżnośćmethod jakand ithe wykorzystaniesecant informacjimethod, ooffering kształcieboth funkcji.convergence and the use of information about the shape of the function.

DziałIt works by iteratively narrowing the interval where the function changes sign, implying the existence of a ona na zasadzie iteracyjnego zawężania przedziału, w którym funkcja zmienia znak, co oznacza istnienie pierwiastkaroot (naby mocythe twierdzeniamean ovalue wartości średniej)theorem). WAt każdejeach iteracjiiteration, obliczanythe jestintersection punktof przecięciathe cięciwychord poprowadzonejdrawn przezthrough końcethe przedziałuends zof osiąthe Xinterval —with the x-axis is calculated—this is the so-called "false entry." Then a new subinterval is chosen where the function continues to tzw.change „fałszywasign.

pozycja”. Następnie wybierany jest nowy podprzedział, w którym funkcja nadal zmienia znak.

 Task 2 

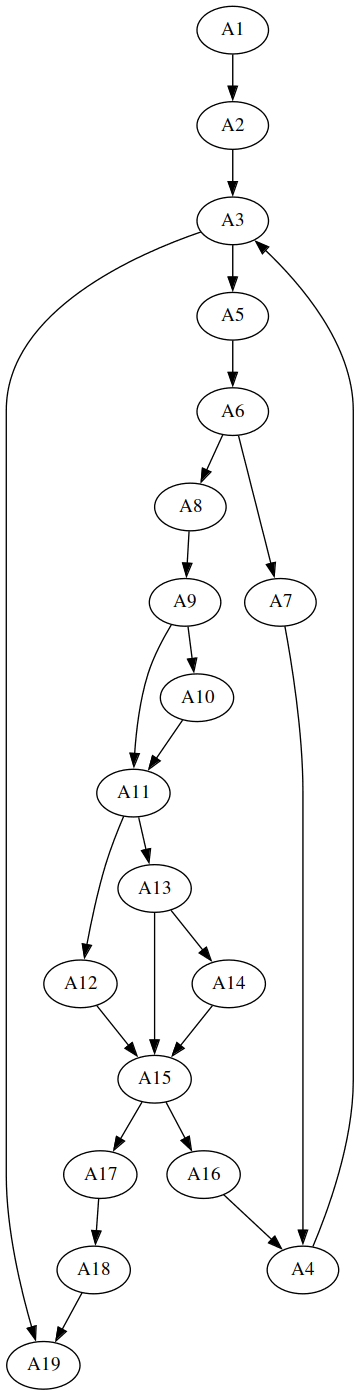
 source code with annotated instructions + Control Flow Graph 

#include <stdio.h>
#include <math.h>

double f(double x) {
   return cos(x) - x*x*x;
}
/* a,b: endpoints of an interval where we search
   e: half of upper bound for relative error
   m: maximal number of iteration
*/
double FalsiMethod(double (*f)(double), double a, double b, double e, int m) {
   double c, fc;
   int n, side = 0;
   /* starting values at endpoints of interval */
   double fa = f(a);
   double fb = f(b);

   for (n = 0; n < m; n++) {
      c = (fa * b - fb * a) / (fa - fb);
      if (fabs(b - a) < e * fabs(b + a))
         break;
      fc = f(c);

      if (fc * fb > 0) {
         /* fc and fb have same sign, copy c to b */
         b = c; fb = fc;
         if (side == -1)
            fa /= 2;
         side = -1;
      } else if (fa * fc > 0) {
         /* fc and fa have same sign, copy c to a */
         a = c; fa = fc;
         if (side == +1)
            fb /= 2;
         side = +1;
      } else {
         /* fc * f_ very small (looks like zero) */
         break;
      }
   }
   return c;
}

int main(void) {
   printf("%0.15f\n", FalsiMethod(&f, 0, 1, 5E-15, 100));
   return 0;
}

1	double c, fc; int n, side = 0; double fa = f(a); double fb = f(b); A1
2	for (n = 0A2; n < mA3; n++A4) {
3	c = (fa * b - fb * a) / (fa – fb); A5
4	if (fabs(b - a) < e * fabs(b + a)) A6
5	Break; A7
6	fc = f(c); A8
7	if (fc * fb > 0) A9 {
8	b = c; fb = fc; A10
9	if (side == -1) A11
10	Fa /= 2; Side = -1; A12
11	} else if (fa * fc > 0) A13{
12	a = c; fa = fc; A14
13	if (side == +1) A15
14	Fb /= 2; Side = +1; A16
15	} else { A17
16	Break; A18
17	}
18	}
19	return c; A19