Example - Regula Falsi method

Task 1 

The Regula Falsi method is a numerical technique for finding zeros of a continuous function on a given interval. It combines the advantages of the bisection method and the secant method, offering both convergence and the use of information about the shape of the function.

It works by iteratively narrowing the interval where the function changes sign, implying the existence of a root (by the mean value theorem). At each iteration, the intersection of the chord drawn through the ends of the interval with the x-axis is calculated—this is the so-called "false entry." Then a new subinterval is chosen where the function continues to change sign.

 Task 2 

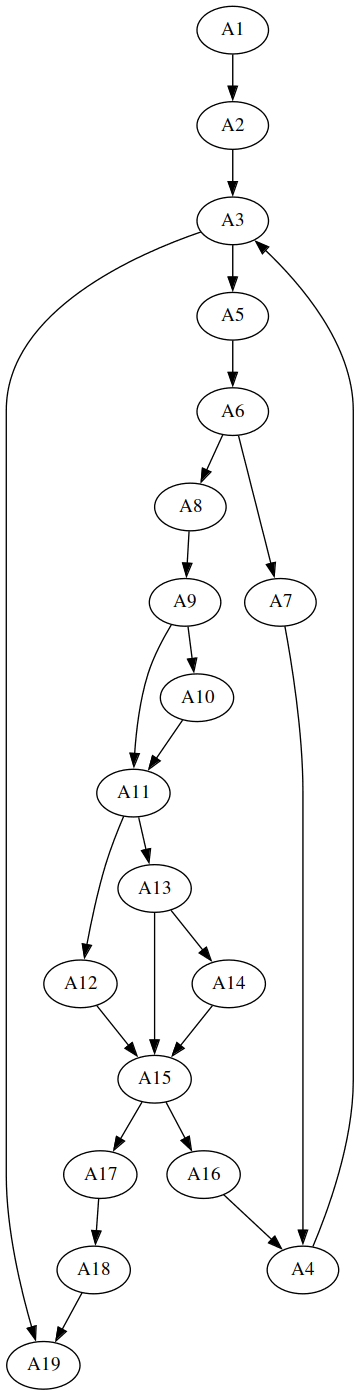
 source code with annotated instructions + Control Flow Graph 

#include <stdio.h>
#include <math.h>

double f(double x) {
   return cos(x) - x*x*x;
}
/* a,b: endpoints of an interval where we search
   e: half of upper bound for relative error
   m: maximal number of iteration
*/
double FalsiMethod(double (*f)(double), double a, double b, double e, int m) {
   double c, fc;
   int n, side = 0;
   /* starting values at endpoints of interval */
   double fa = f(a);
   double fb = f(b);

   for (n = 0; n < m; n++) {
      c = (fa * b - fb * a) / (fa - fb);
      if (fabs(b - a) < e * fabs(b + a))
         break;
      fc = f(c);

      if (fc * fb > 0) {
         /* fc and fb have same sign, copy c to b */
         b = c; fb = fc;
         if (side == -1)
            fa /= 2;
         side = -1;
      } else if (fa * fc > 0) {
         /* fc and fa have same sign, copy c to a */
         a = c; fa = fc;
         if (side == +1)
            fb /= 2;
         side = +1;
      } else {
         /* fc * f_ very small (looks like zero) */
         break;
      }
   }
   return c;
}

int main(void) {
   printf("%0.15f\n", FalsiMethod(&f, 0, 1, 5E-15, 100));
   return 0;
}