Example - Regula Falsi method

Task 1 

Metoda Regula Falsi to numeryczna technika służąca do znajdowania miejsc zerowych funkcji ciągłej w danym przedziale. Łączy ona zalety metody bisekcji i metody siecznych, oferując zarówno zbieżność jak i wykorzystanie informacji o kształcie funkcji.

Działa ona na zasadzie iteracyjnego zawężania przedziału, w którym funkcja zmienia znak, co oznacza istnienie pierwiastka (na mocy twierdzenia o wartości średniej). W każdej iteracji obliczany jest punkt przecięcia cięciwy poprowadzonej przez końce przedziału z osią X — to tzw. „fałszywa pozycja”. Następnie wybierany jest nowy podprzedział, w którym funkcja nadal zmienia znak.

 Task 2 

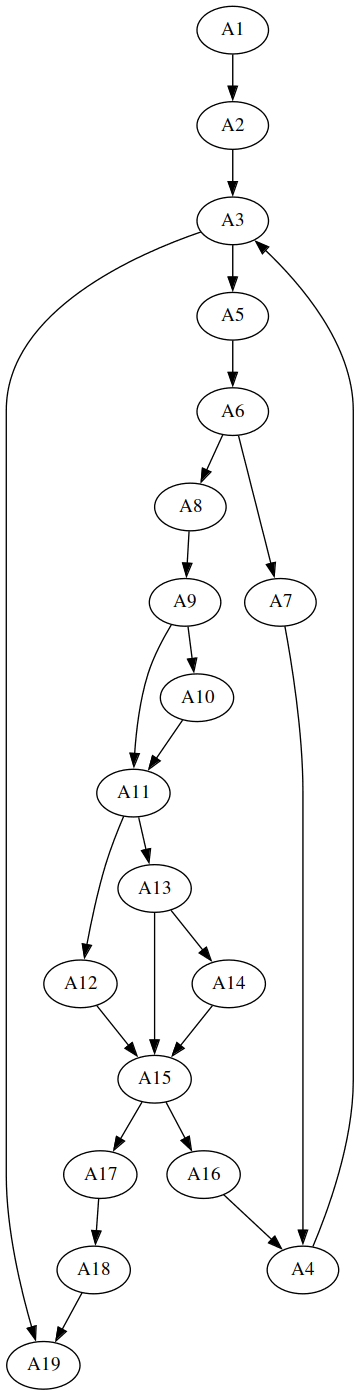
 source code with annotated instructions + Control Flow Graph 

#include <stdio.h>
#include <math.h>

double f(double x) {
   return cos(x) - x*x*x;
}
/* a,b: endpoints of an interval where we search
   e: half of upper bound for relative error
   m: maximal number of iteration
*/
double FalsiMethod(double (*f)(double), double a, double b, double e, int m) {
   double c, fc;
   int n, side = 0;
   /* starting values at endpoints of interval */
   double fa = f(a);
   double fb = f(b);

   for (n = 0; n < m; n++) {
      c = (fa * b - fb * a) / (fa - fb);
      if (fabs(b - a) < e * fabs(b + a))
         break;
      fc = f(c);

      if (fc * fb > 0) {
         /* fc and fb have same sign, copy c to b */
         b = c; fb = fc;
         if (side == -1)
            fa /= 2;
         side = -1;
      } else if (fa * fc > 0) {
         /* fc and fa have same sign, copy c to a */
         a = c; fa = fc;
         if (side == +1)
            fb /= 2;
         side = +1;
      } else {
         /* fc * f_ very small (looks like zero) */
         break;
      }
   }
   return c;
}

int main(void) {
   printf("%0.15f\n", FalsiMethod(&f, 0, 1, 5E-15, 100));
   return 0;
}

1	double c, fc; int n, side = 0; double fa = f(a); double fb = f(b); A1
2	for (n = 0A2; n < mA3; n++A4) {
3	c = (fa * b - fb * a) / (fa – fb); A5
4	if (fabs(b - a) < e * fabs(b + a)) A6
5	Break; A7
6	fc = f(c); A8
7	if (fc * fb > 0) A9 {
8	b = c; fb = fc; A10
9	if (side == -1) A11
10	Fa /= 2; Side = -1; A12
11	} else if (fa * fc > 0) A13{
12	a = c; fa = fc; A14
13	if (side == +1) A15
14	Fb /= 2; Side = +1; A16
15	} else { A17
16	Break; A18
17	}
18	}
19	return c; A19