Centrality of eigenvectors

Definition

Eigenvector centrality is one measure of centrality in network analysis. It determines how important (central) a node (e.g., a person, an organization) is in a network, taking into account not only the number of its connections, but also the quality of those connections - that is, how important the nodes to which it is connected are.

A node has high centrality if it is connected to many other important nodes.

Unlike degree centrality, which counts the number of neighbors, eigenvector centrality also takes into account their influence.

Mathematical context

Eigenvector centrality has its basis in linear algebra and uses concepts such as neighborhood matrix and values and eigenvectors.

a) The neighborhood matrix (A)
For a given network (such as a social graph), a neighborhood matrix is created:

This is a square matrix A, in which:

A[i][j] = 1, if there is a connection between node i and j,

A[i][j] = 0, if there is no such connection.

For an undirected network, the matrix is symmetrical.

b) Centrality formula
We are looking for a vector x such that:

A ⋅ x = λ ⋅ x

,where:

x is the centrality vector (each element is the centrality value of a given node),

λ is the largest eigenvalue (dominant),

A is the neighborhood matrix.

In other words: the centrality of a node depends on the sum of the centrality of its neighbors.

c) Interpretation of the formula
This formula means that:

A node has high centrality if it is connected to other nodes that themselves have high centrality.

Solving this equation provides a fixed point in the propagation of influence in the network.

Graphic example with explanation

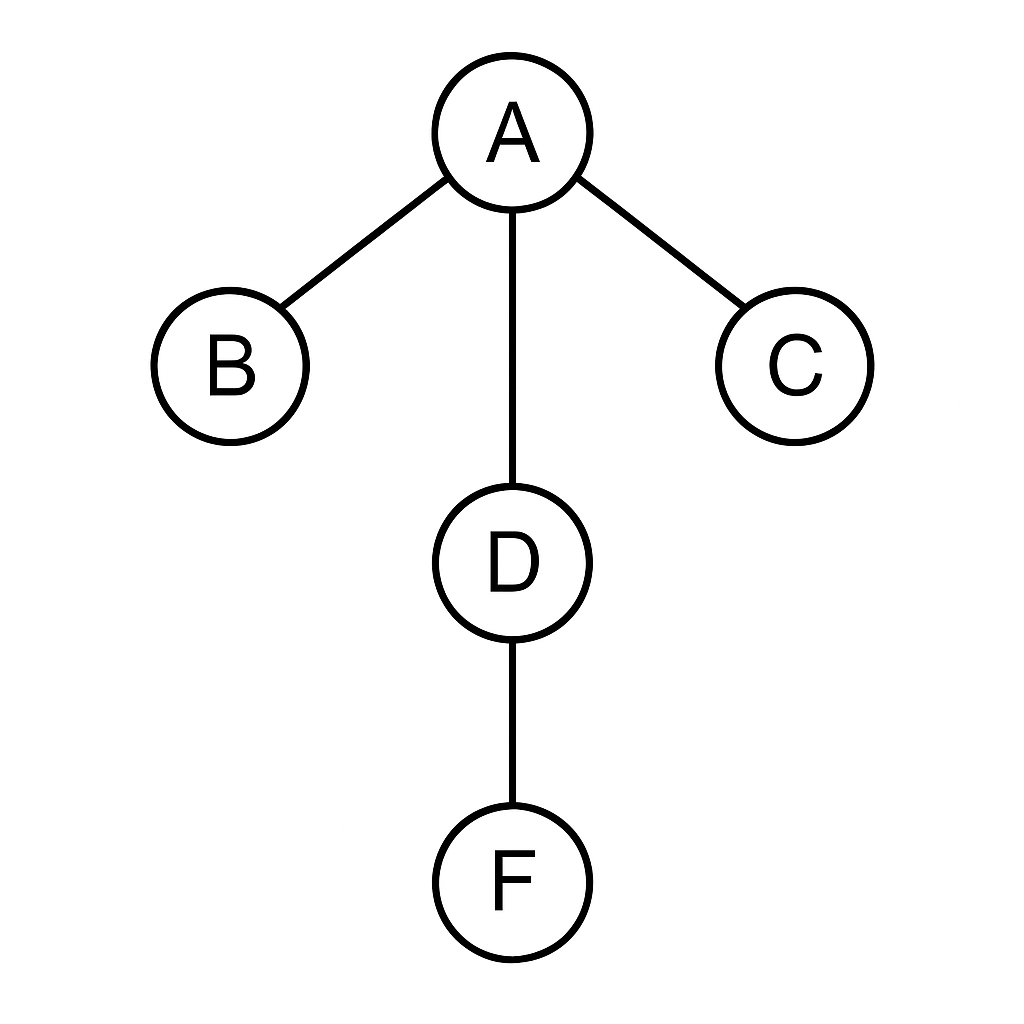
To better understand what eigenvector centrality is, let's look at a simple network of nodes:

Fig. 1 Example network

Network structure:
The network consists of 6 nodes:

A is the central node, connected to nodes B, C and D.

D, in turn, leads on to E and F.

The connections (edges) are undirected, which means that the relationships are reciprocal (e.g., “A knows B” is the same as “B knows A”).

What can be observed?

A is directly connected to three nodes - B, C and D.

D acts as a bridge between the central A and the distant nodes E and F.

F is the outermost - it is connected only to E, which in turn is connected only to D.

How does eigenvector centrality work in this network?

Node A:
- Has a high degree (3 connections),
- It is connected to other important nodes (D leads to more nodes),
- As a result, its eigenvector centrality will be the highest.

Nodes B and C:
- Each has only one connection - to A,
- Although A is important, the lack of their own downstream connections lowers their centrality.

Node D:
- Has a connection to A (important), but also to E,
- Its centrality will be medium - it depends on the position of its neighbors.

Nodes E and F:
- Are located on the periphery of the network,
- They are connected by only one link,
- Their centrality will be the lowest.

What does this example show?

The centrality of eigenvectors is all about structural context - who is connected to whom, and how important the neighbors are.

A node can be important even if it has few connections itself - if its neighbors are very influential.

This shows that the “loudest” node (with the most connections) is not always the most influential one - the quality of the network around it matters.

Interpretation of eigenvector centrality

Eigenvector centrality is a measure that goes a step further than simply counting connections (such as the degree of a node). Its main advantage is that it takes into account the quality of connections, not just the number of them.

What is the essence of this centrality?
Eigenvector centrality assigns each node a value that reflects not only how many connections it has, but to whom it is connected:

If a node is connected to other nodes with high centrality, its own centrality also increases.

Similarly, being connected to insignificant nodes will not significantly increase its centrality.

The intuition behind this measure:
Imagine that in a social network:

Person A knows five people who are very well connected to others and have important roles in the organization.

Person B knows ten people, but each is rather isolated and has little influence.

Even though B knows more people, A will have a higher centrality of self vectors because he knows more influential people.

Differences from other measures:

Measure	What does it measure?	Example
Centrality of degree	The number of direct connections	How many friends do you have
Centrality of agency	How often a node mediates paths between others	Are you a “connector” between groups
Centrality of proximity	How close you are to all other nodes	How quickly you can reach everyone
Centrality of eigenvectors	How influential your connections are	Are your friends influential

What do centrality values mean?
Centrality values are usually normalized to the range [0, 1].

A node with a value close to 1 is strongly embedded in the core of the network.

A node with a value close to 0 is at the periphery of the network or connected only to weakly significant nodes.

Interpretive benefits:

Allows you to see who is really influential - not just who knows the most people, but who knows the right people.

Useful in analyzing informal structures, where the real power of a person/group is not always due to formal position.

Practical applications

Eigenvector centrality finds application in various fields: